Which casino games offer the best chances to win

Even though casino gambling should always be done just for fun and entertainment, players are of course interested in winning. There are many different types of games you can play that work in different ways. Therefore, many players want to know which casino games offer the best chances of winning.
In this guide, we’ll take a look at what it means to “win” while playing games at the casino. We’ll also analyse the most popular types of casino games to see which offer the best odds.
Understanding how games work
Factors that can influence strategies and decisions while playing casino games can be written in mathematical and statistical terms. For this guide, we’ll call these objective factors.
This objective information provides gamblers with an exact mathematical description of how each game works. Players can then make comparisons between the games, or between different situations within the same game. This can form the basis for a playing strategy, including when to choose one game over another.
Within each game’s design, the “chances of winning” are the most sought-after and are expressed in terms of odds and probabilities.
What does winning actually mean?
Since odds and probabilities are a measure for the chance, likelihood, or trust that certain events will happen, it’s fair to use odds and probabilities as the basis for which casino games offer the best chances of winning.
However, we must first define what “chances of winning” means in the context of gambling.
Probabilistic chances of winning

One way of looking at it is to consider individual (one-off) bets on their own, such as:
- Winning a street bet in roulette
- Winning a pass line bet in craps
- Hitting a winning combination on the payline of a slot machine
In these cases, all other factors are not considered – such as past or future bets, how much is staked, profits and losses, and so on.
Instead, winning is the direct consequence of an isolated gaming event happening. The “chances” for them to happen are given by precise probabilities. In this context, “chances” has the mathematical meaning of classical probability. In casino games, the probability of an event is the ratio between:
The number of situations favourable for that event to occur and the total number of equally-possible situations.
This basic definition of probability is enough to measure the chances of winning any bet in whatever casino game. However, we must clearly establish what the equally-possible situations are. In probability-theory terms, this is the sample space for each experiment.
For example, in Roulette, the sample space is the set of all roulette numbers that are all equally possible. In European roulette, the numbers range from 0 – 36. This means there are 37 different possible outcomes of each spin.
To win a bet on the 1st dozen in European roulette, the result would need to be one of: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, or 12.
So the probability of winnings this bet is 12/37 = 32.43%.
In this case, the chances of winning are determined by the outcome of the game – not how much is staked on the bet. We can call this “probabilistic chances of winning”.
Expectation-based chances of winning
Another way of defining “chances of winning” is to consider all gambling activity over a certain period of time, or the number of games played.
You compare your overall profits vs overall losses.
If you have won more than you have lost then this is considered a win overall.
The length of time can be in the short, medium, or long run.
In this context, the probability of winning isolated (one-off) bets is no longer the only factor that counts when assessing the chances of winning. That’s because “winning” in this case also has a monetary sense.
Of course, we can estimate the probability of winning certain isolated bets over the entire gambling period. But this is not the only factor. Because if you win certain isolated bets – but lose overall – then it is not considered a win.
Expected value (EV)
Although this definition of “winning” results from subtracting losses from winnings for an overall profit, the “chances of winning” in this context are still related to probability. That’s because probability is the only adequate measure for the random events.
The mathematical notion of the expected value (EV) of a bet has the following basic definition:
EV = (probability of winning) × (payoff if you win) + (probability of losing) × (loss if you lose).
The EV of a bet is interpreted as the amount you may expect to win or lose on average if playing that bet indefinitely many times, over the long run, or infinitely many times in mathematical terms.
Of course, the EV of a bet should be negative. That’s so the house is guaranteed a profit.
On average, you will lose a certain amount for every bet over the long run. But of course you may win at any time or make a profit over a definite number of plays.
House edge (HE)
House edge (HE) is defined as the opposite of the expected value. It suggests the rate of profit that the house (casino) will make over the long run from player bets.
For each game, the statistical average of the house edge of all possible bets is called the house edge of that game. It is specific to any game and can be used to estimate the “chances of winning” in this context of the term.
The house edge should be positive for the house not to go bankrupt in the long run.
The higher the house edge, the lower the chances of winning are for the player.
Both EV and HE are known as statistical averages. This means they do not apply to specific periods of time (such as individual gaming sessions of players).
In these cases, the chances of winning are a measure of the whole game itself – not for isolated (one-off) outcomes. We can call this “expectation-based chances of winning”.
Now we’ve established the two main meanings for “chances of winning”, let’s see which casino games offer the highest chances for both.
What casino game has the highest probability of winning?

For most casino games, bets can be placed directly on physical outcomes. This includes numbers, totals, symbols, etc – such as in Roulette, Craps, and slots. In other games, bets can be placed on beating the dealer – such as in Blackjack.
For either category, the winning odds can be mostly found using probability computations.
Slots
The only exception is slots. That’s because the wide majority of slot providers keep their game configurations a secret – such as the distribution and weighting of the symbols on the reels. Without this information, it’s not possible to compute the probability of any given winning combination in the prize schedule of that game.
Information about the mathematical design of a slot game is rarely retrieved. Sometimes this is due to legal intervention. But other times it’s due to statistical experiments that aim to “deconstruct” a slot machine. These experiments need many thousands of actual spins to be observed and recorded.
Statistical experiments provide gambling experts with approximate probabilities of winning for many slot games. The general finding was that such probabilities are very low.
The probability is not just low for the big-prize combinations either, but also for smaller prizes.
Here’s an example of the probability table for the Double Strike slot game by IGT, obtained after recording about 4000 spins:
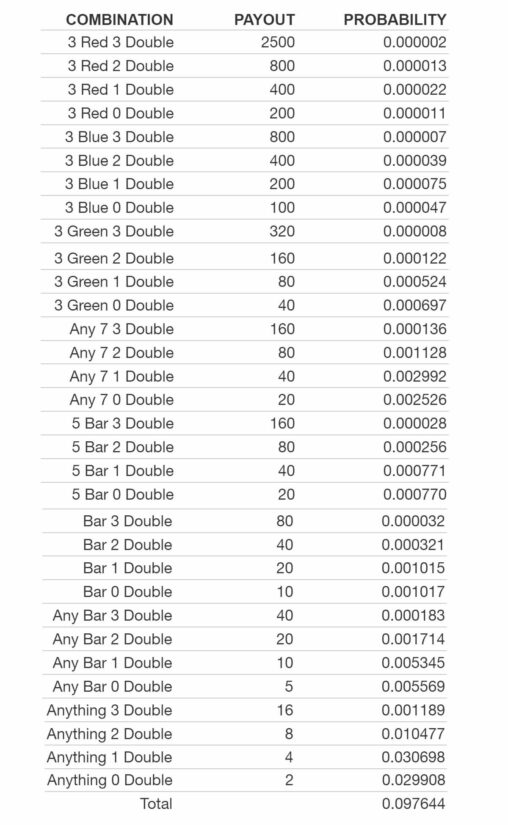
As shown, the 3 lowest-prize combinations have probabilities ranging between 1-3%. The probability for the top prize is 0.000002%.
Of course, there are thousands of slot games on the market. Some other slots may have winning probabilities that are higher. But it’s fair to assume that these games offer winning odds in the same order of magnitude. That’s because a slot game is designed for the player to spin tens or hundreds of times in a playing session, while the total number of possible combinations is huge.
We can fairly see slots as a candidate for the last position in the winning odds ranking.
Craps
If we look at the winning odds in two-dice games such as craps, they are significantly higher than in slots:
| Event | Probability |
|---|---|
| 2 points | 2.77% |
| 3 points | 5.55% |
| 4 points | 8.33% |
| 5 points | 8.33% |
| 6 points | 13.88% |
| 7 points | 16.66% |
| 8 points | 13.88% |
| 9 points | 11.11% |
| 10 points | 8.33% |
| 11 points | 5.55% |
| 12 points | 2.77% |
The chances of winning a bet in craps – for either pass line, don’t pass line, or the point – do not go below 2.77%. One outcome also has a probability of 16.66%.
Blackjack & Baccarat
For Blackjack, the winning odds can be far more difficult to obtain when playing with actual stacks of cards. That’s because previous rounds have occurred which will impact the probability of the current round.
However, here are some basic Blackjack odds (in decimal format) for the player’s hand to win based on the dealer’s first card:
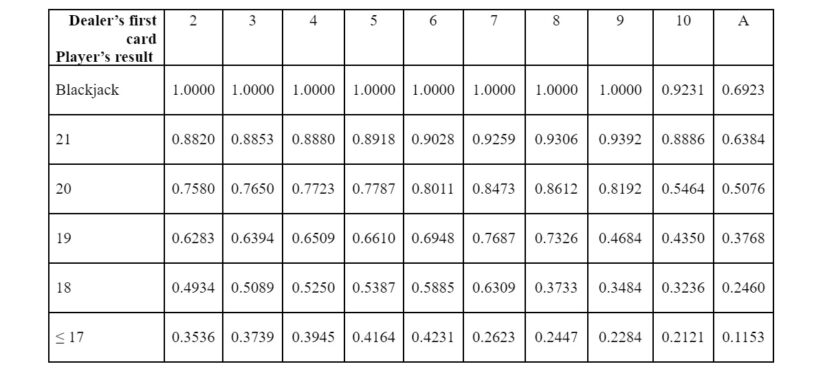
When the player has a high starting hand (most notably from 19 through to Blackjack), the winning probabilities are very good. But of course, these are the most advantageous situations.
The most frequent starting hands in Blackjack are 18, 17, or below. These winning odds range from 11.53% to 63.09%.
So although Blackjack offers very high winning probabilities (up to 100%), this is not quite relevant to our ranking of casino games offering the best chance of winning. That’s because the highest winning probabilities associated with a game should not be conditional, but general.
So it’s necessary to base the highest chances of winning in a game on general play, before playing it.
The raw estimation of winning a round of Blackjack before any cards have been dealt is 42.43%.
So we credit Blackjack with this winning probability for our ranking – while keeping in mind that cards dealt during the game may give winning odds above 90%.
In Baccarat, the raw estimation of winning a bet is a bit higher at 44.67%. So it’s pretty similar to Blackjack.
Roulette
The odds of winning simple bets on Roulette depend on which type of Roulette you play.
- European Roulette (37 possible outcomes)
- Straight-up bet: 2.70%
- Even-money bet: 48.64%
- American Roulette (38 possible outcomes)
- Straight-up bet: 2.63%
- Even-money bet: 47.36%
So there are close to 50% winning odds for even-money bets – such as red/black, even/odd, low/high. This puts Roulette slightly ahead of Blackjack in our ranking.
But how does Roulette compare with Blackjack’s most advantageous starting hands?
Roulette can actually provide winning odds of >90% thanks to a feature that no other casino game has.
At each spin, a player may place combined bets in whatever number and configuration they want on the betting table.
The probability of winning one of these combined bets increases linearly based on the coverage of that bet. So if players decide to cover more numbers across the table, the winning probability will increase.
But there are two things to keep in mind about placing large-coverage bets in roulette:
- Contradictory bet: Covering as many numbers as possible must not be done chaotically. Otherwise you may see a contradictory bet – which is a bet that has no profit whatever the outcome of the spin.
- Low-profit rate: A high probability of winning is counterbalanced by a low-profit rate. It’s a principle that applies to all casino games – and it ensures the house advantage remains constant and favourable for the casino.
So what’s the ideal balance between high probability and low-profit?
A large-coverage combined bet that offers the highest winning odds is one where the player bets on a colour and then makes several straight-up bets on numbers of the opposite colour.
In the next table, we’ll take a look at the odds and profits/losses of large-coverage bets on American Roulette, including the following parameters:
- n – The number of straight-up bets
- The range chosen was between 15 and 17 for the highest winning odds. Anything over 17 for n becomes a contradictory bet.
- S – The stake on each straight-up bet
- c – Ratio between the stake on the colour bet and the stake on a straight-up bet
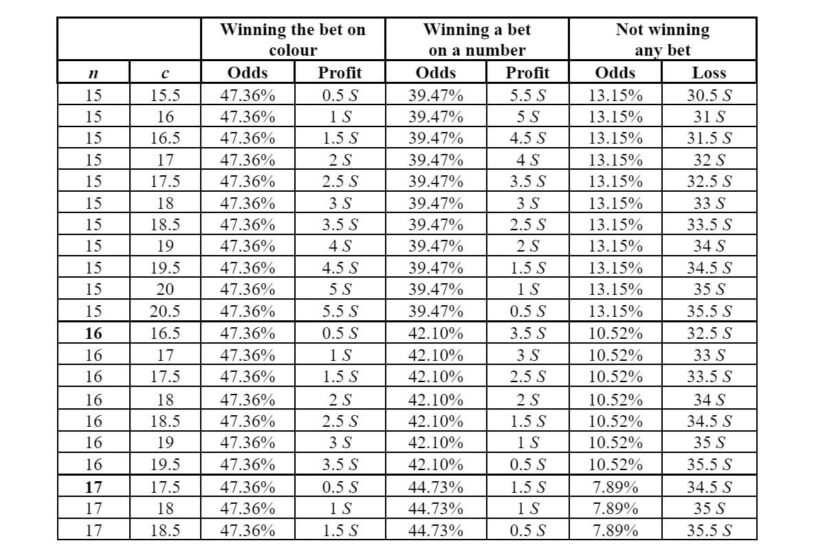
The highest odds of winning on Roulette is when n = 17. So when 17 straight-up bets are placed.
This results in odds of 47.36% + 44.73% = 92.09%. In European Roulette, the odds are slightly higher at 94.59%.
However, the possible profit is between 0.5 to 1.5 times the stake on the color bet. Also, the risk of losing outright has a probability of 7.89% – which is over 34 times the stake.
The same odds apply when combing straight-up bets with other even-money bets – like low/high or odd/even.
Other large-coverage bets are available, but those mentioned before offer the highest odds of winning.
So overall, European Roulette tops the list of casino games that give the best chance of winning when using the above method. No other casino game will offer you winning odds for a once-placed bet higher than 94.59%.
Best casino game odds
When thinking about chances of winning in terms of attempted profit over the long run (or minimising the overall loss), all casino games are ranked by their house edges.
The house edge of a game varies depending on the game’s rules. That’s why the house edge can change for different versions of a game.
But the strategy that players use can also affect the house edge. Strategies that are mathematically conceived (based on probability and expectation comparisons) cannot increase the odds of winning. However, they can minimise loss and maximise profit over the long run, where applicable. But only Blackjack allows such strategies.
Roulette
| Bet | House edge |
|---|---|
| Any bet in classical European roulette | 2.70% |
| Any bet in classical American roulette | 5.26% |
| Non even-money bet in French roulette | 2.70% |
| Even-money bet in French roulette with La Partage or En Prison | 1.35% |
You can see that the house advantage is higher in American Roulette compared with European Roulette and French Roulette.
The lowest possible house edge for Roulette is the French version under specific circumstances.
Craps
| Bet | House Edge |
|---|---|
| Pass Line | 1.41% |
| Don't Pass Line | 1.36% |
| Come | 1.41% |
| Don't Come | 1.36% |
| Place Bets | 6.7% 4% 1.5% |
| Buy Bets 5% Commission | 4.76% |
| Lay Bets 5% Commission | 2.44% 3.23% 4% |
| Big 6 or 8 | 9.09% |
| Field Bets | 5.56% |
| Hardways | 11.1% 9.09% |
| Any 7 | 16.9% |
| Any Craps | 11.1% |
| Proposition 2 or 12 | 13.9% |
| Proposition 3 or 11 | 11.1% |
So there’s a clear spread for the house edge in craps – ranging between 1.36% and 13.9%.
Blackjack
| Game | House edge |
|---|---|
| Atlantic City Blackjack | 0.36% |
| American Blackjack | 0.35% |
| Big Five Blackjack | 0.47% |
| Classic Blackjack | 0.13% |
| Double Exposure | 0.69% |
| European Blackjack | 0.42% |
| Pontoon | 0.41% |
| Premier Blackjack | 0.42% |
| Spanish Blackjack | 0.38% |
| Super Fun 21 | 0.94% |
| Vegas Downtown Blackjack | 0.39% |
| Vegas Single Deck Blackjack | 0.35% |
| Vegas Strip Blackjack | 0.35% |
This is the lowest house edge of all. None of the games give the casino an advantage of over 1%.
If you are able to deploy optimal strategies (such as fixed strategy and high-low-count) then the house edge values above get even lower.
Baccarat
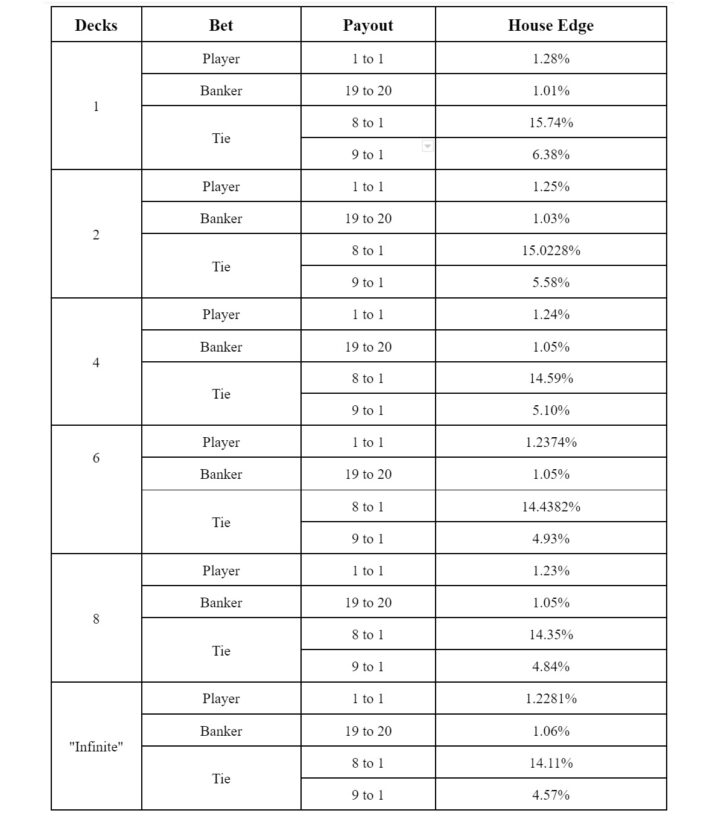
The house edge in baccarat varies slightly based on the number of card decks that are being used.
Slots
For slots, it’s difficult to give exact numbers for the house edge as the exact parameters of these games are not always known.
Many slot providers and casinos use the statistical indicator RTP (return to player) percentage. In this case, the house edge is the different between 100% and the RTP amount. For example:
- A typical slot has an RTP between 94% and 97%
- The house edge for this range would be between 6% and 3%
Conclusion
So the casino games with the best chances of winning overall are:
- Isolated (one-off bets): Roulette (winning odds of >90%)
- Long run: Blackjack (lowest house edge of <1%)
For isolated (one-off) bets, Roulette offers the best chance of winning with probabilities over 90% when using optimal large-coverage bets. The downside is that these odds have a low-profit rate.
In the long run, Blackjack offers the best chance of winning with a house edge of under 1% for all variations of the game. This house edge can even be reduced when using optimal strategies.
References
- Bărboianu, C. (2007). Roulette Odds and Profits – The Mathematics of Complex Bets. Infarom.
- Bărboianu, C. (2022). Understanding Your Game: A Mathematician’s Advice for Rational and Safe Gambling. PhilScience Press.
- Bewersdorff, J. (2021). Luck, Logic, and White Lies: The Mathematics of Games, second edition. CRC Press.
- https://probability.infarom.ro
