¿Qué es la probabilidad condicionada y cómo usarla para tus apuestas?

¿Alguna vez te has preguntado cómo los apostadores profesionales toman decisiones más inteligentes? La probabilidad condicionada es una herramienta matemática poderosa que puede ayudarte a calcular las probabilidades de un evento a partir de información previa, algo clave en apuestas deportivas y juegos de casino. En este artículo, te explicaremos qué es la probabilidad condicionada, cómo calcularla y cómo aplicarla en póker, blackjack, ruleta o apuestas en vivo. Con ejemplos prácticos, pasos claros y consejos útiles, esta guía te brindará las herramientas para apostar con mayor confianza y estrategia en 2025. ¡Sigue leyendo y descubre cómo dominar la probabilidad condicionada para mejorar tus resultados!
Definición de probabilidad condicionada
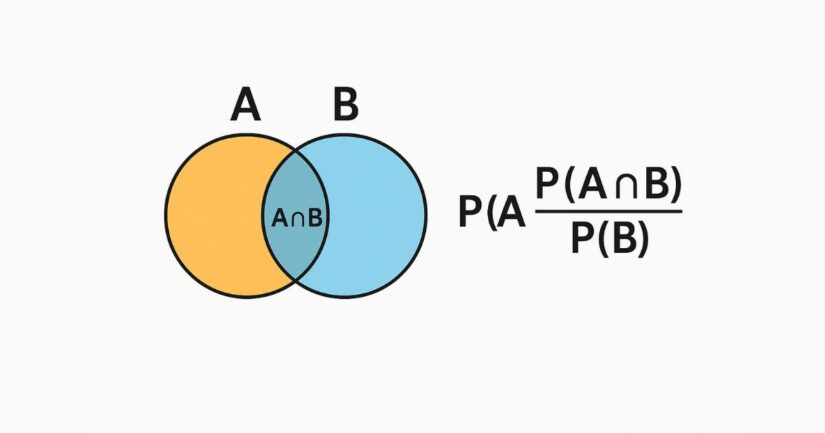
La probabilidad condicionada es la probabilidad de que ocurra un evento A, dado que ya ha ocurrido otro evento B. En términos simples, se trata de calcular las posibilidades ajustadas a la nueva información. Matemáticamente, se expresa como:
P(A|B) = P(A ∩ B) / P(B)
Donde:
P(A|B) es la probabilidad de A dado B.
P(A ∩ B) es la probabilidad de que ocurran ambos eventos.
P(B) es la probabilidad del evento condicionante.
Por ejemplo, imagina un mazo de 52 cartas. Si sacas una carta y es un corazón, la probabilidad de que la siguiente carta sea un as cambia porque ya sabes que hay un corazón menos. Esto es probabilidad condicionada en acción.
A diferencia de la probabilidad simple, que no considera eventos previos, la probabilidad condicionada ajusta los cálculos según lo que ya ha ocurrido. En las apuestas, esto es crucial. Por ejemplo, en póker, si ves que se han repartido ciertas cartas, puedes calcular mejor las probabilidades de completar tu mano. En apuestas deportivas, si un equipo anota primero, las probabilidades de que gane el partido cambian.
| Concepto | Definición | Ejemplo |
|---|---|---|
| Probabilidad Simple | Posibilidad de un evento sin condiciones | Probabilidad de sacar un as (4/52). |
| Probabilidad Condicionada | Posibilidad ajustada por un evento previo | Probabilidad de sacar un as sabiendo que la carta es un corazón (1/13). |
En el mundo de las apuestas, la probabilidad condicionada te ayuda a tomar decisiones más informadas, ya sea en un casino o durante un partido en vivo. A continuación, exploraremos por qué es tan importante.
¿Por qué es importante la probabilidad condicionada en las apuestas?
La probabilidad condicionada es fundamental porque te permite tomar decisiones más informadas a partir de la información previa. Es especialmente relevante en juegos como el póker o el blackjack, donde las cartas reveladas modifican las probabilidades. Además, es útil en las apuestas deportivas, especialmente en tiempo real.
Por ejemplo, si un equipo recibe una tarjeta roja, las probabilidades cambian, y la probabilidad condicionada te ayuda a recalcular.
En póker, si sabes que alguien ha descartado cierta carta, puedes ajustar tus cálculos y determinar si tu mano es más fuerte. En blackjack, los jugadores que cuentan cartas usan este tipo de probabilidad para determinar si deben pedir otra carta. En deportes, si un equipo anota en los primeros 10 minutos, es más probable que gane, lo que cambia las cuotas.
¿Por qué usarla?
- Te ayuda a tomar decisiones basadas en hechos, no en la intuición.
- Te permite ajustar tu estrategia a medida que avanza el juego.
- Reduce el riesgo de apostar por impulso.
Calcular la probabilidad condicionada: paso a paso
Calcular la probabilidad condicionada no es tan complicado como parece. Aquí tienes una guía paso a paso:
Paso 1: Identifica los eventos
Define el evento que quieres calcular (A) y el evento condicionante (B). Por ejemplo:
- A: Que un equipo gane un partido de fútbol.
- B: Que el equipo haya anotado el primer gol.
Paso 2: Calcula la probabilidad conjunta (P(A ∩ B))
Determina la probabilidad de que ambos eventos ocurran simultáneamente. Por ejemplo, si el 30% de los partidos en los que un equipo anota primero terminan en victoria, entonces P(A ∩ B) = 0.30.
Paso 3: Calcula la probabilidad del evento condicionante (P(B))
Encuentra la probabilidad de que ocurra el evento B. Si el 50% de los partidos tienen un primer gol de un equipo específico, entonces P(B) = 0.50.
Paso 4: Aplica la fórmula
Usa la fórmula P(A|B) = P(A ∩ B) / P(B). En el ejemplo:
P(A|B) = 0.30 / 0.50 = 0.60 o 60%.
| Paso | Descripción | Ejemplo |
|---|---|---|
| 1 | Identificar eventos | A: Real Madrid gana, B: Anota primero |
| 2 | Calcular P(A ∩ B) | 40% de victorias con primer gol |
| 3 | Calcular P(B) | 60% de partidos con primer gol |
| 4 | Aplicar fórmula | P(A |
Con esta base, veamos cómo aplicar la probabilidad condicionada en juegos de casino específicos.
Ejemplos de probabilidad condicionada en juegos de casino
La probabilidad condicionada brilla en los juegos de casino donde la información parcial cambia las probabilidades. A continuación, exploramos cómo se aplica en póker, blackjack y ruleta mediante ejemplos detallados.
Póker: calculando la probabilidad de una mano
En el póker, la probabilidad condicionada es clave para evaluar tus posibilidades a partir de las cartas visibles. Supongamos que estás jugando Texas Hold’em y buscas completar un color (flush) de corazones. Tienes dos corazones en tu mano y el flop también muestra dos corazones.
- Evento A: la próxima carta (turn) es un corazón.
- Evento B: ya se han repartido cuatro corazones (dos en tu mano, dos en el flop).
- Hay 13 corazones en un mazo de 52 cartas. Como ya se han usado 4, quedan 9 corazones.
- Total de cartas restantes: 52 – 5 (tus dos cartas + tres del flop) = 47.
- P(A|B) = 9/47 ≈ 0.191 o 19,1 %.
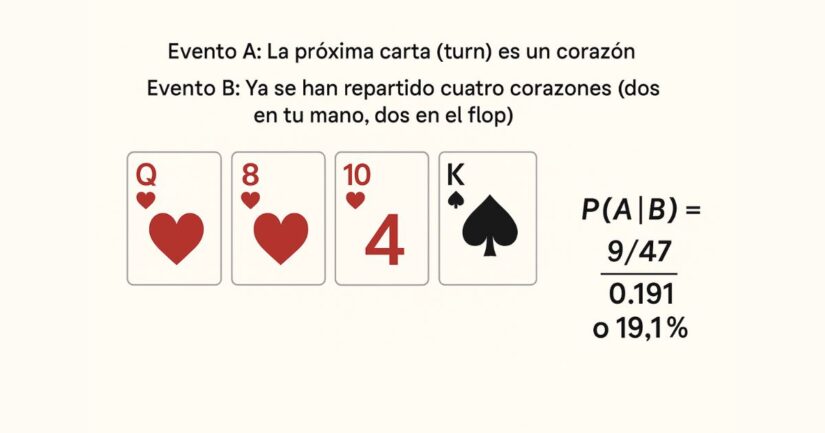
Esto significa que tienes un 19,1 % de probabilidad de conseguir un corazón en el turn, lo que puede guiar tu decisión de apostar o retirarte.
Blackjack: contando cartas
En el blackjack, la probabilidad condicionada es fundamental para los jugadores que cuentan cartas. Si sabes qué cartas han sido repartidas, puedes calcular con mayor precisión la probabilidad de recibir una carta específica. Por ejemplo:
- Quieres saber la probabilidad de recibir un 10 (10, J, Q, K) para llegar a 21.
- Supongamos que se han repartido 20 cartas de un mazo de 52 y 5 de ellas eran 10.
- Quedan 16 10s (4 de cada J, Q, K, 10) en 32 cartas.
- P(10|B) = 16/32 = 0.50 o 50%.
Con un 50% de probabilidad, podrías pedir otra carta si tu mano lo permite.

Para más estrategias de blackjack, consulta nuestra Guía de blackjack online.
Ruleta: Limitaciones de la probabilidad condicionada
En la ruleta, cada giro es independiente, por lo que la probabilidad condicionada tiene un uso limitado. Por ejemplo, la probabilidad de que salga rojo no cambia aunque los últimos 10 giros hayan sido negros. Sin embargo, algunos jugadores usan sistemas como el Martingale, ajustando las apuestas según los resultados previos, aunque esto no altera las probabilidades reales.
| Juego | Aplicación de Probabilidad Condicionada | Ejemplo |
|---|---|---|
| Póker | Calcular probabilidad de manos según cartas visibles | 19.1% de completar un color |
| Blackjack | Contar cartas para decidir acciones | 50% de recibir un 10 |
Probabilidad condicionada en apuestas deportivas: casos reales

En las apuestas deportivas, especialmente en las en vivo, la probabilidad condicionada es una herramienta poderosa para ajustar tus decisiones según el desarrollo del evento. Las cuotas cambian en tiempo real según eventos como goles, tarjetas o lesiones, y entender estas probabilidades te da una ventaja.
Caso práctico: fútbol
Imagina un partido entre Manchester City y Liverpool. Quieres apostar a que Manchester City ganará, pero el partido está empatado al medio tiempo. Sin embargo, Liverpool recibe una tarjeta roja, lo que reduce su equipo a 10 jugadores.
- Evento A: Manchester City gana.
- Evento B: Liverpool tiene 10 jugadores.
Según datos históricos, en el 70% de los partidos en los que un equipo pierde a un jugador, el equipo contrario gana (P(A ∩ B) = 0.70).
Un equipo recibe una tarjeta roja en el 20% de los partidos (P(B) = 0.20).
P(A|B) = 0.70 / 0.20 = 3.5, pero como las probabilidades no pueden exceder 1, ajustamos los datos. Supongamos que P(A ∩ B) = 0.14 y P(B) = 0.20; entonces, P(A|B) = 0.14 / 0.20 = 0.70 o 70%.
Esto sugiere que Manchester City tiene un 70% de probabilidad de ganar, lo que puede justificar una apuesta en vivo.
Herramientas útiles
Algunas casas de apuestas ofrecen calculadoras de probabilidades o estadísticas en tiempo real. Aplicaciones como Bet365 o William Hill proporcionan datos sobre posesión, tiros al arco y más que puedes usar para estimar probabilidades condicionadas.
Consejos para usar la probabilidad condicionada al apostar
- Usa datos históricos: analiza estadísticas de equipos, jugadores o juegos para estimar probabilidades condicionadas.
- Practica con juegos gratis: juega póker o blackjack en modo demo para familiarizarte con los cálculos.
- Mantente actualizado: en apuestas en vivo, sigue las estadísticas en tiempo real para ajustar tus probabilidades.
- Evita las decisiones emocionales: confía en los números, no en corazonadas.
- Establece un presupuesto: la probabilidad condicionada mejora tus decisiones, pero no elimina el riesgo.
- Consulta herramientas: usa calculadoras de probabilidad o apps de apuestas para agilizar los cálculos.
- Juega responsablemente: nunca apuestes más de lo que puedes permitirte perder.
La probabilidad condicionada no garantiza ganancias, pero sí te da una ventaja competitiva. Para más estrategias, explora las guías de Casino Professor y comienza a apostar con inteligencia.
Preguntas frecuentes sobre la probabilidad condicionada
¿Qué es la probabilidad condicionada en apuestas?
¿Cómo se calcula la probabilidad condicionada?
¿Es útil la probabilidad condicionada en los juegos de casino?
¿Puedo usar la probabilidad condicionada en apuestas en vivo?
¿Cuál es un ejemplo claro de probabilidad condicionada?
Conclusión: usa la probabilidad condicionada como herramienta de apuestas inteligentes
La probabilidad condicionada no es un truco complicado. Es una forma simple de ajustar tus apuestas a medida que va surgiendo la información real.
No necesitas ser un experto en matemáticas para usarla. Basta con entender que cada nuevo dato puede cambiar las probabilidades y que los mejores apostadores saben aprovecharlo.
